A to Z
Annotation
Results of the metabolite-derived peaks are compared and matched with the results (m/z, MT) from standard reagents that were measured beforehand. The metabolite names are assigned to the detected peaks; this is known as “annotation”. The set of results obtained by measuring the standard reagents is called the “annotation list” or “library”.
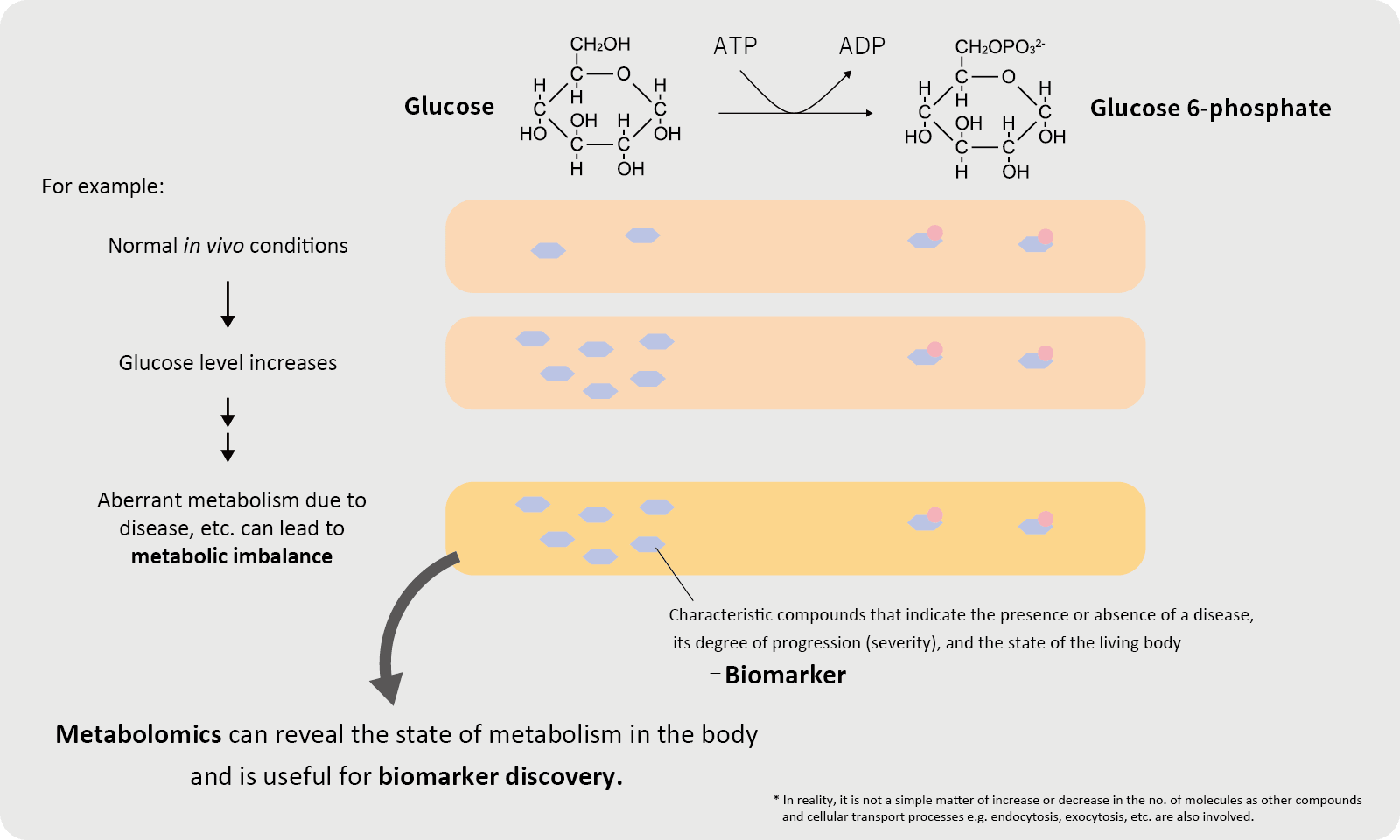
Biomarkers
Biomarkers are measurable substances such as genes, proteins, and metabolites that are found in the body. Biomarkers fluctuate in correlation with biological information, for example, changes in diseases and responses to treatment, and can be objectively evaluated as response indicators.
Calculated concentration (absolute quantification)
Since absolute quantification determines the metabolite concentration, it is possible to compare different metabolites, add or subtract certain metabolites (e.g., for calculation of total amino acids or branched chain amino acids, etc.) and compare analysis data from different batches. Thus, allowing the calculation of metabolic parameters and integration with previous analysis data.
Flux analysis
An analysis of metabolic fluxes using stable isotopes.
By adding substrates labeled with stable isotopes of carbon atoms (or nitrogen atom) at specific sites, it is possible to determine the metabolic pathway that was taken; this is not achievable with just a general metabolome analysis. Flux analysis can be applied to designing metabolism to improve the efficiency of the production of useful compounds.
HCA
An abbreviation for Hierarchical Cluster Analysis.
HCA is an analysis method that classifies factors that are mathematically similar with respect to a group of data of interest. Metabolites with similar patterns of relative values among samples are classified based on the standardized values of metabolomic measurements (relative or absolute), and the results are represented in a heat map.
Heat map
A data visualization method in which individual values aligned in two-dimensional data (matrix) are expressed as colors or shades according to the magnitude of the values.
HPLC
An abbreviation for High Performance Liquid Chromatography.
HPLC is a type of separation method known as column chromatography, in which a sample solution (mixture) is passed through a stationary phase (column) in a mobile phase flow and separated using the velocity difference in the column passage caused by the affinity between the column and the substance, and further analyzed at high speed by applying pressure.
Chromatography refers to the physical method of separation, while chromatogram refers to the visual output, and chromatograph refers to the instrument.
Mass Spectrometry (MS)
Mass spectrometry (MS) is an analytical technique in which a sample is ionized, and the ions produced are separated by the action of an electric or magnetic field to obtain an m/z value. Compounds with similar molecular weights can be separated by passing the sample through a separator before it reaches the mass spectrometer.
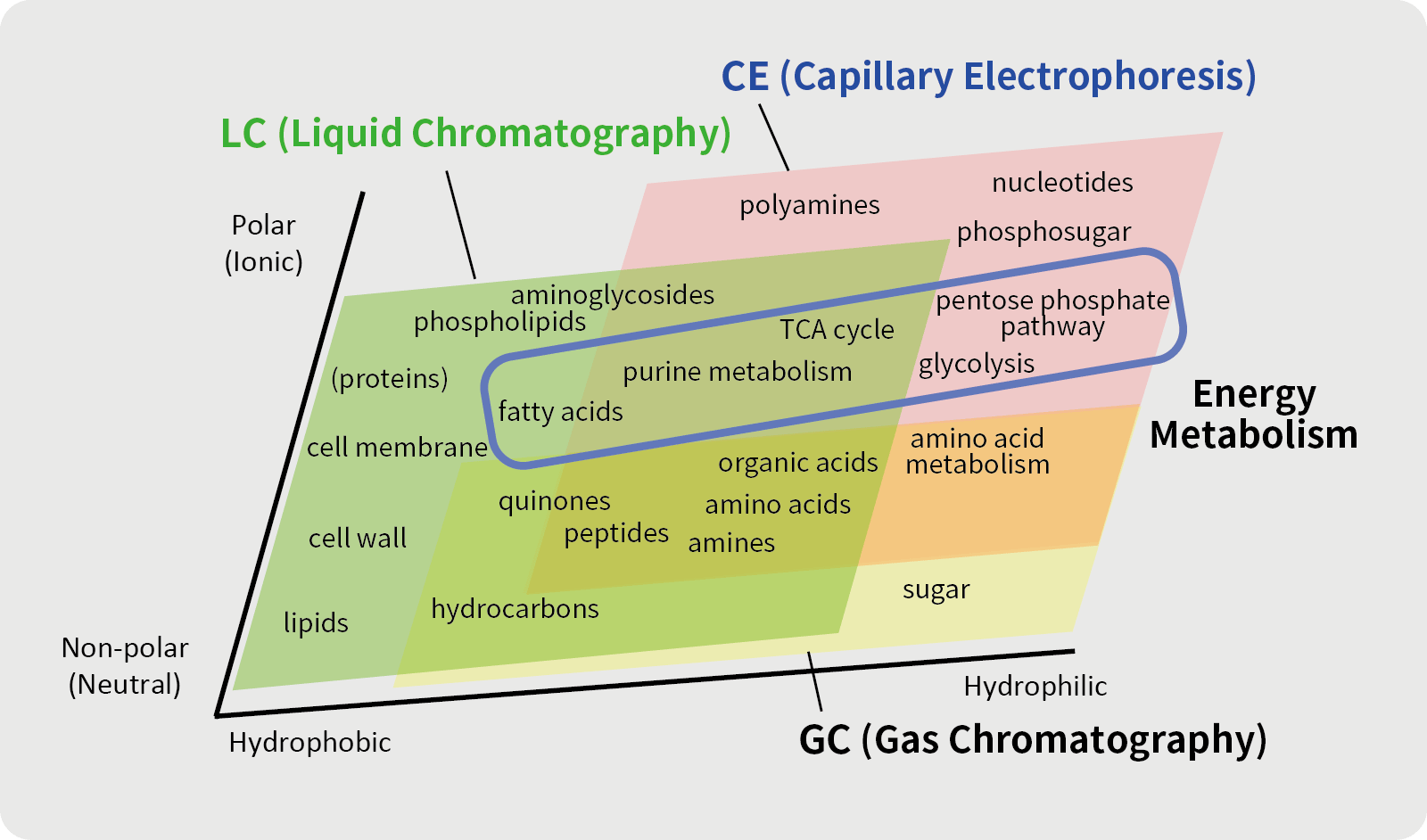
Separation methods are selected according to the nature of the compounds. Capillary electrophoresis (CE) separates ionic compounds at high speed and with high resolution by applying high voltage to both ends of a very thin tube i.e., capillary. Liquid chromatography (LC) uses the principle that molecular retention differs between the stationary and mobile phases, and gas chromatography (GC) separates molecules in a gaseous state and is suitable for gaseous or volatile compounds.
Mass spectrum
A graph of the relative ion intensity (signal intensity) versus the m/z value obtained from mass spectrometry. The signal on a mass spectrum is known as the peak.
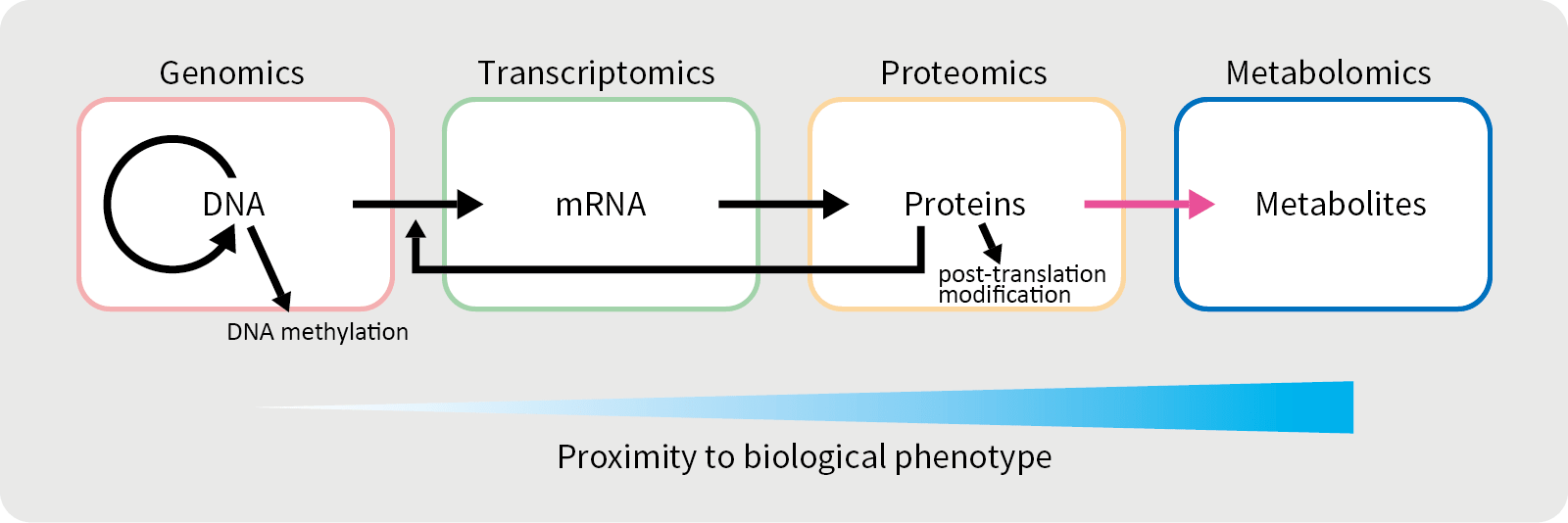
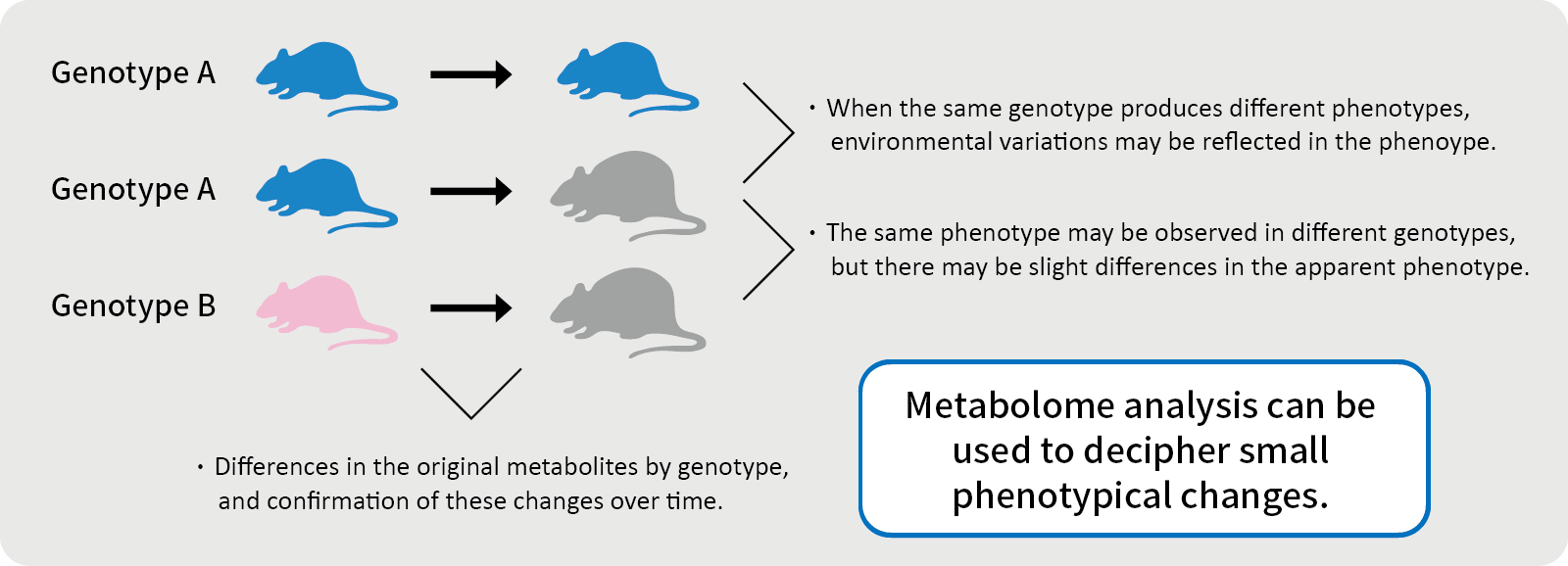
Metabolome / Metabolomics
“Omics” is composed of the Greek suffix “ome”, which means “totality”, and “ics”, which means “study”, and is used as a collective term for a study of the totality of a given field. In order words, metabolomics is an omics of metabolites and it refers to a method of comprehensively analyzing the types and concentrations of metabolites. It is also a general term for low molecular weight metabolites in living organisms.
In recent years, “multi-omics”, which is a comprehensive analysis of multiple areas such as genes, proteins, gene expression, and metabolites, have also been actively used to characterize complex diseases and improve personalized medicine.
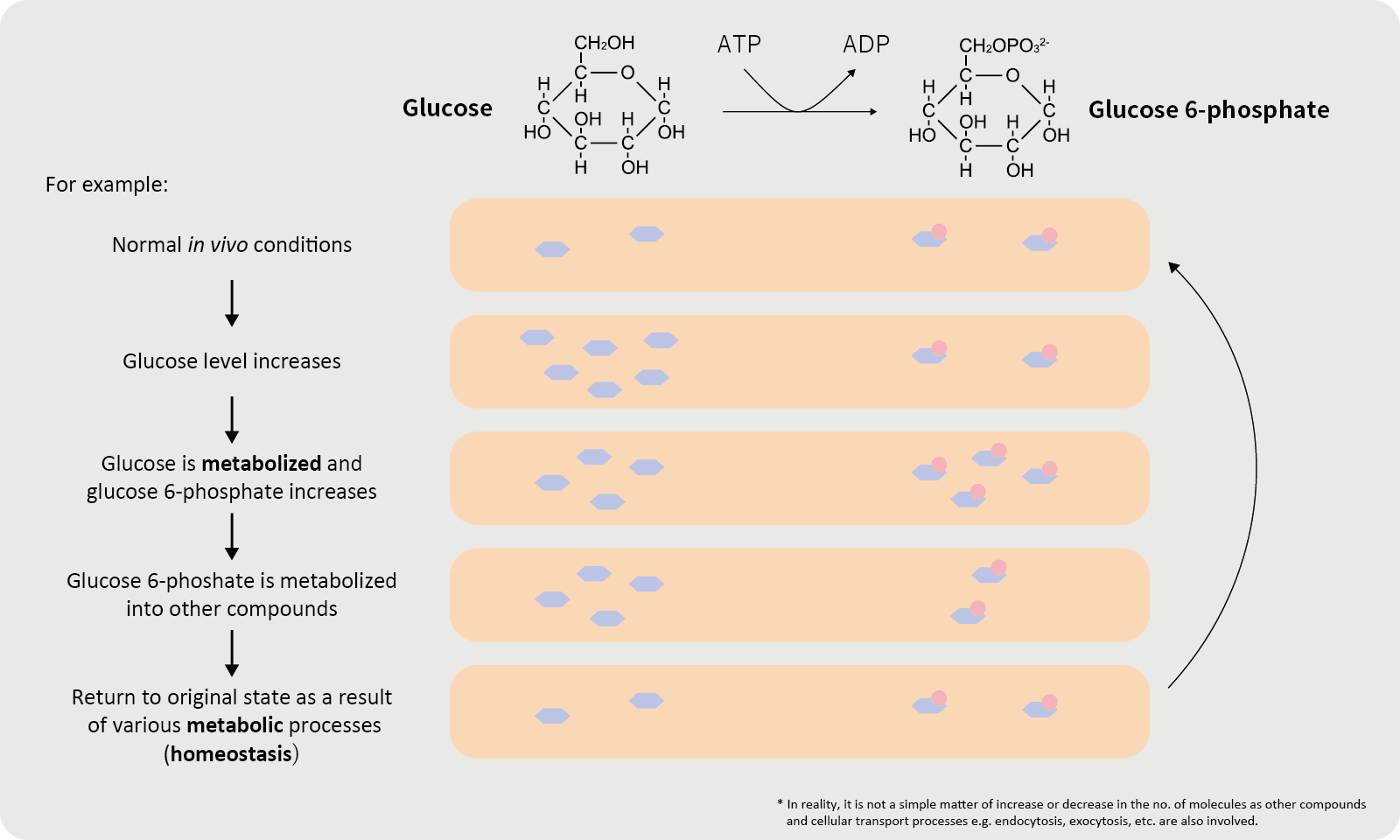
Metabolism
Metabolism refers to the chemical reactions that synthesize and break down metabolites through the action of enzymes and coenzymes in the body. The properties of the metabolites in a given specimen are known as the “metabolic profile”.
The process that produces metabolites (e.g., sugars, proteins, lipids, and nucleic acids) that are involved in normal growth, development, and reproduction of organism is called primary metabolism. Secondary metabolism, on the other hand, generates the end products of primary metabolism. The changes in the state of metabolites are known as “metabolic changes”.
Metabolic pathway
A metabolic pathway is a representation of a series of metabolic interactions occurring within a cell. A depiction of multiple metabolic pathways together is called a “pathway map”.
Typical examples of metabolic pathways include glycolysis, which breaks down glucose to produce pyruvate and ATP, and the TCA cycle (citric acid cycle), which plays an important role in energy production and is closely related to other pathways such as amino acid metabolism and urea cycle. These energy-producing pathways are collectively referred to as central carbon metabolism.
Metabolites
Metabolites are intermediates or end products of metabolism. There are two types of metabolites: hydrophilic (water-soluble) and ionic metabolites with a high affinity to water, and lipophilic (fat-soluble) metabolites with a high affinity to lipids. Depending on the nature of the metabolites, different analytical instruments are used to measure the metabolites of interest.
MT/RT
MT (Migration Time) refers to the time from the sample starts to travel down the capillary during CE until it is detected by the mass spectrometer.
RT (Retention Time) is the time taken from sample injection into the column to the time it is eluted during LC.
Each molecule has a unique MT or RT depending on its physical properties.
m/z
m/z is a dimensionless quantity obtained by dividing the mass of an ion by the unified atomic mass unit, followed by the charge number of the ion.
In mass spectrometry, molecules are separated according to the ratio of mass to charge; therefore, m/z becomes the measurement value.
PCA
An abbreviation of Principal Component Analysis.
The data generated in metabolomics is multi-dimensional, with rows corresponding to samples or subjects and columns corresponding to metabolite features (or vice versa). Therefore, it is difficult to intuitively grasp the characteristics or “metabolic profile” of each sample from the obtained data. PCA refers to a statistical analysis method that abstracts the entire data by reducing the dimensions of such data and displays it in a visually comprehensible plot.
Pre-processing (Pre-treatment)
The process of stopping metabolism by inactivating enzymes through protein denaturation, etc. and removing compounds that interfere with mass spectrometer measurements and extracting metabolites.
For CE-MS, pre-processing methods vary depending on the analytical instrument used, such as deproteinization and removal of phospholipids.
Relative area (relative quantification)
Absolute quantification is a method used in metabolome analysis to measure the metabolite amount in a sample by creating a calibration curve derived from known concentrations of the metabolite. On the other hand, in relative quantification, a calibration curve derived from known concentration of another reference metabolite is created, and the relative amount of the target metabolite present in the sample is quantified in relation to that metabolite. The relative metabolite amount ratio (e.g., metabolite X is twice as high in group A compared to group B) can be determined by observing the difference in the relative amounts of the target metabolites between samples based on the relative quantification value.
Targeted analysis/ Non-targeted analysis
Choose either targeted or non-targeted analysis to suit your research purpose.
If the target metabolite is known, choose targeted analysis for detailed structural analysis and group comparison, which are performed by focusing on the peaks found in the annotation list; this is based on the presumption that those peaks correspond to the target metabolites in your sample.
If the target metabolite is unknown, for example, in biomarker search, choose non-targeted analysis, in which peaks are compared between the samples to find those that characterize the differences between groups.
Resources
For more detailed information, download our Service Leaflets from the following page:

Download
Home