研究開発本部の山本です。
前回までは、主成分分析の因子負荷量が、主成分スコアと各代謝物質レベルとの(ピアソンの)相関係数で定義されること、またソフトウェアによって因子負荷量の定義が異なるので、使用される際にはお使いのソフトウェアをご確認していただく必要があることをご説明しました。
今回は、因子負荷量の仮説検定を用いて、代謝物質を選択する方法についてご紹介します。
初めに、一般的な相関係数の仮説検定についてご説明します。まず、相関係数rを以下の式でt値に変換します。
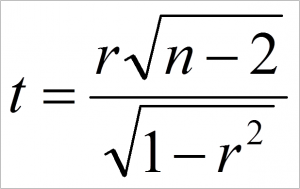
ここで、nはサンプルサイズ(全サンプル数)を表しています。得られたt値は、自由度n-2のt分布に従うことが知られており、この性質を利用してp値を計算することが出来ます。
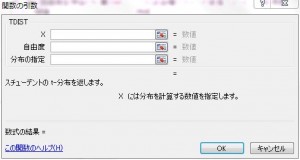 計算は非常に簡単です。Excelを用いて計算をする場合は、関数tdist(t,自由度,2)で計算することが出来ます。上式の相関係数rから計算したt値、自由度はn-2、最後の2は両側検定のための設定値です。
計算は非常に簡単です。Excelを用いて計算をする場合は、関数tdist(t,自由度,2)で計算することが出来ます。上式の相関係数rから計算したt値、自由度はn-2、最後の2は両側検定のための設定値です。
他にも、相関係数を計算するとp値を一緒に計算してくれるものもあります(Rの関数のcor.testなど)ので、お好きなものを使って計算していただければと思います。
以上が相関係数の仮説検定の計算方法です。
同様に、主成分スコアと各代謝物質レベルとの相関係数である因子負荷量のp値も計算することが出来ます。多重検定を考慮する場合は、より厳しい基準のボンフェローニの補正やq値を用います。
得られたp値(もしくはq値)から、有意水準5%未満のものを有意な代謝物質とし、選択した代謝物質について生物学的な解釈を行っていくことで統計学的な裏付けのある考察となります。
主成分分析の因子負荷量とは何か、また因子負荷量の仮説検定をご紹介してきましたが、今回で主成分分析の説明は終わりです。次回以降は、実際のメタボロームデータの解析例についてご紹介したいと思います。
最後に、10月1~2日に行われる第9回メタボロームシンポジウムのインフォマティクスのセッション(10月2日11:10~12:30)で、主成分分析とPartial least squaresの因子負荷量の仮説検定について口頭発表する予定です。興味のある方は是非お立ち寄りください。
