研究開発本部の山本です。前回は主成分スコアプロットとローディングプロットをどのように利用するか、その見方についてご紹介しました。

今回は、前回説明したローディングについて、生物学的解釈につなげていくために「ローディングの中身」についてご説明したいと思います。

ローディングと一口に言っても、英語ではloading、PCA loading、factor loading、weight vector、eigenvector、日本語では因子負荷量、主成分負荷量、など実は様々あるのですが、混同されていることが多いです。今回は、「因子負荷量（factor loading）」と言われているものについて考えていきましょう。

主成分分析は、理論的にはデータの分散共分散行列の固有値問題で表され、その”固有ベクトル”を計算し、さらにそこから主成分スコアが計算されます。多くの論文でこの”固有ベクトル”が因子負荷量として使われています。これは、メタボロミクスでよく用いられているソフトウェア（例えばUmetrics社のSIMCAや、MetaboAnalyst）がそのようになっているからだと思います。HMTの受託解析の報告書もこれに倣っています。

この「固有ベクトル」とは、いったい何なのでしょうか。

Wikipediaでは、「線型変換の固有ベクトルとは、その変換後に単に大きさが定数倍されるだけの影響しか受けない（倍率が1ならまったく影響を受けない）ベクトルのことである」と説明されています。確かに学生の時に先生からそのように教わりましたし、その通りなのですが、だから何なの？どう使えば良いの？そんなことよりももっと実践的に教えて欲しい！というのが皆さんのご意見なのではないかと思います。

では、ここからはより生物学的な解釈がしやすい捉え方をご紹介します。

実は、主成分分析の固有ベクトルは、データをautoscalingした場合（MetaboAnalystではData scalingをAutoscalingに設定した場合）に限り、主成分スコアと各代謝物質レベルとの相関係数に比例することが知られています。このことから、統計や多変量解析の分野では、主成分分析の因子負荷量の定義として主成分スコアと各代謝物質レベルとの相関係数が用いられることが多いです。

相関係数とは、みなさんもよくご存知の通り、2つの変数（代謝物濃度など）の散布図を書いた時に、右肩上がりに直線に並べば+1、右肩下がりに直線に並べば-1になります。変数間に線形関係が無ければ0に近くなる指標です。

因子負荷量＝相関係数であれば、その値をある程度統計的な基準で見ることができます。

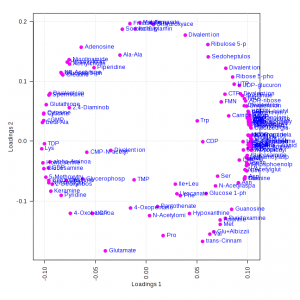例えば、前回の記事で作成したローディングプロット（左図）の縦軸と横軸のスケールを見ると、それぞれ±0.2と±0.1になっています。

ローディングの値が相対的に大きな代謝物質を選択する、ということはできますが、何個まで取ればよいのか、また値はいくつまで着目すればよいのかは明確ではありません。

一方で相関係数の場合には（理論的にそれが正しいかは置いておいて）実務的には0.7以上で相関が高い、0.3以下だと相関が弱いだろうといった感覚によって、因子負荷量を用いて代謝物質を選択することができます。

以上のことから、特にメタボロームデータを解析する際には、因子負荷量 (factor loading) は主成分スコアと各代謝物質レベルとの相関係数であると考えていただくと生物学的な解釈もやりやすいのではないかと思います。

後篇では実際に、MetaboAnalystの因子負荷量の結果と、相関係数で定義される因子負荷量の結果を比較してみます。