バイオメディカルグループ(統計解析)の山本です。前回までは, 主に多変量解析を用いたメタボロームデータ解析について説明してきました. 多変量解析は回帰・判別モデルの構築や, データの視覚化には有効ですが, ある現象に特に大きく関わっている単一もしくは2,3の物質を特定することが目的であるバイオマーカー探索では, 単変量毎に仮説検定等を行うのがより直接的なアプローチです. そこで今回は, 主にバイオマーカー探索における統計的仮説検定に関する話をいくつか紹介したいと思います.
はじめに, 統計的仮説検定の考え方を簡単に説明します. 2群間の差に関する仮説検定では, まず群間で差が無いという仮説(帰無仮説)を立てます. 実験して得られたデータは, その差がない仮説の下で得られたとします. その時の差がない仮説が支持される確率がp-valueです. p<0.05とは, 5%以下の確率で差がないので, 2群間に差があるだろうと判断します. もう少しわかりやすく説明するために, t検定を例にして説明します. t検定では, 2群間で差が有るか無いかは, 群間の平均の差とデータのばらつき(分散)とサンプル数(t分布の自由度)によって決まります. 2群間に差がありかつばらつきが小さければ, その差は将来何回同じ実験をしてデータを取っても起こりうる差だろうし, 逆に2群間に差があったとしても, ばらつきが大きければ, その差は信頼できなくなります. またサンプル数が小さい場合よりも大きい方が, 同じ差であればよりその差は信頼できます. t検定のp-valueは, これらを含んだ差の尺度となっています.
1. なぜ多重比較が必要か? p-valueの補正もしくはq-valueはなぜ必要か?
ここまで古典的な仮説検定について説明してきました. しかしこれをそのままオミクスデータのバイオマーカー探索に適用するには少し抵抗があります. 何故なら, バイオマーカー探索においては, ある特定の物質がその他の物質に比べて差が大きいかを知りたいわけで, 単純に単一の物質のデータだけを見ればよいわけではないからです. そこで, 全ての物質について差が無いという仮説の下で, 特定の物質に差があるかどうかを調べるために, オミクスデータの仮説検定では, 多重比較の考えの下p-valueの補正やq-valueが用いられます. 次に, 多重比較について簡単に説明します.
簡単にするために, データセット全体で3個の物質(物質A,B,C)があるとします. 仮説検定が1つの時, 大雑把に言えば, 有意水準が5%では, 差がない確率は0.95, 差がある確率は0.05です. これをそのまま多重比較にあてはめてみます. 物質Aで2群間に差が無いときに, 物質B,Cに差がある・差がない, というパターンには次の4つが考えられます.
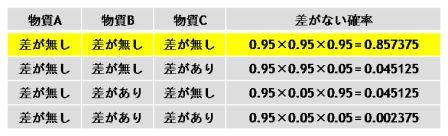
この4つのケースで差がない確率の和を計算すると,
0.857375+0.045125+0.045125+0.002375=0.95となり, 差がある確率は1-0.95=0.05となります. つまり, 多重比較の問題に有意水準5%そのままあてはめると, これらの4つのパターン全てで差がある確率が5%になっていることがわかります.
しかし今我々は, A,B,C全てに差がなく, それが物質Aについてのみ棄却される確率(黄色部分)を知りたい, と先程述べました. その場合には, 差がない確率は0.857375, 差がある確率は0.1426となり, 有意水準を14.26%に設定していることに相当します. 差が無いことが起こる確率が小さい(5%)から差があると結論付ける仮説検定で, 差が無いことが起こる確率が14%では, 差があると言えなくなってしまいます.
そこで, 有意水準を, 元の有意水準5%を物質数3で割った5/3=1.6667%に設定して、同じ計算をしてみます.
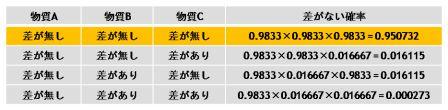
この場合, A,B,C全てに差がなく, それが物質Aについてのみ棄却される確率(オレンジ色部分)は0.950732, 差がある確率は0.0493となり, めでたく約5%有意水準になっていることがわかります. これがbonferroniによるp-valueの補正です.
以上の統計的仮説検定における多重比較とそれに基づくp-valueの補正では, 複数の仮説検定がある場合に, それをファミリーと考え, ファミリー全体での誤りFWER(family-wise error rate)が5%になるようにp-valueを補正することで, より適切な確率の値を算出することが出来ます. しかしこの方法は, αエラーを小さくしているけれど, βエラーを大きくしてしまう, つまり補正が厳しすぎて, 本来差があるものも差が無いとしてしまうことがある, という問題点が指摘されています. そこで, αエラーだけでなくβエラーも考慮したFDR(False discovery rate)を基準としたq-valueと呼ばれる指標が提案され, オミクスデータの仮説検定ではよく用いられています. 次回は, この辺りの話について説明したいと思います.
[第1回メタボロミクスと統計解析]オミクスデータの判別
[第2回メタボロミクスと統計解析] メタボロームデータと多変量解析
[第3回メタボロミクスと統計解析] メタボロームデータと多変量解析
