バイオメディカルグループ（統計解析）の山本博之です。

細胞内での現象はほとんどの場合、1つの代謝物質によって説明されることはなく、複数の代謝物質とそのネットワークによって説明されます。よって、複数の変数(代謝物質)を使ってデータを表現する多変量解析がその道具として用いられるのは、比較的自然なことだと思います。メタボローム解析では特に主成分分析が用いられる事が多く、論文等でその計算結果を目にされたことのある方も多いと思います。

オミクスデータのような高次元データは視覚的に人が理解できないので、何らかの形で視覚化することが有効です。主成分分析は高次元データを1次元に射影し、その上での分散が最大になるような射影方向をいくつか求め、それらの軸を用いて視覚化します。1次元上での分散が大きな主成分軸は、一般的にデータを良く表現する軸であるとしばしば説明されます。しかしこれは少し説明不足です。

主成分分析に限らず、多変量解析の結果はデータのある側面を表現しているに過ぎません。例えて言うなら、得体の知れない物体(高次元データ)を刀で切って、その断面を見るようなものです。主成分分析は、切った断面の(部分空間上での)面積(分散)が最も大きくなるように、PLS(Partial least squares)は群がよく分かれるような断面を得る方法です。

我々が見ているのはあくまでデータの断面に過ぎず、必ずしもデータの情報を全て表現できるわけではありません。またデータを標準化する/しないで多変量解析を適用する場合や標準化方法の違い、変数選択後のデータであるかどうかによって、その結果の意味が少しずつ異なります。よって、それぞれの目的に応じた方法を選択する必要があります。従来法の中に適した手法が無い場合、新しい多変量解析手法の開発が求められることもあります。

醗酵プロセスの視覚化に適した新しい多変量解析法の開発

メタボローム解析を用いた醗酵プロセスの可視化の目的で、多変量解析を適用した例を一つご紹介します。醗酵プロセスの可視化のためのメタボローム解析では、多くの場合経時変化での代謝物質の変動の様子を見るために、経時的に得られたサンプルのメタボローム解析が行われます。ここで実際に用いたデータは、エタノール醗酵における酵母のメタボロームデータです。データは経時的に取られており、目的は異なる3つの株の醗酵過程における酵母細胞内の代謝の変動を可視化することでした。実際に主成分分析を計算した結果を左図、我々が開発した手法である平滑化主成分分析^[1]を用いて可視化した結果を右図に示します。

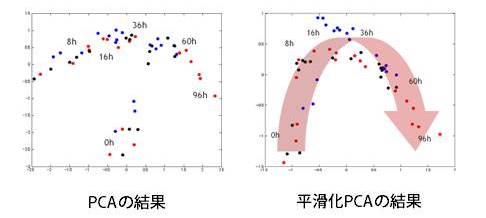
左図の主成分分析の結果に対して、我々の開発した手法では経時変化を見事に捉えることが出来ていることがわかります。先程の喩えで言えば、メタボロームデータという得体の知れない物体を、経時変化の情報が最も大きく得られるような断面で切るための手法を開発し、それが上手く行った例といえます。単に主成分分析を単に適用しただけでは、折角のメタボロームデータが有効活用されないかもしれません。データから情報を最大限引き出す為には、従来の多変量解析をそのまま適用するだけではなく、新たな手法の開発が必要になることもあります。

主成分分析の結果の誤った解釈

次に、主成分分析の結果から誤った結論を導く例をご紹介します。

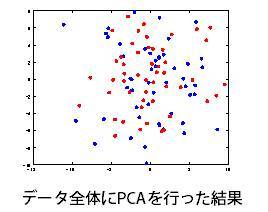
まず、全く同じ分布からランダムにサンプリングされたデータに対して、主成分分析を行った結果を示します。全く同じ分布なので本来1群ですが、便宜上2群のデータとしています。

左図のように群間で差がない結果が得られ、元々の意図した通りメタボロームデータでは2群間に差がない、という正しい結論に至ります。次に全く同じデータから、2群間の平均値の差が10以上(fold change=10)の代謝物質を選択して、データセットを作ります。このデータセットに主成分分析を行った結果を示します。

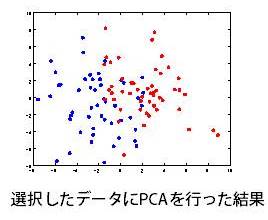
結果からわかるように、元々データ全体としては差が無かったはずが、差が大きなものだけを選択してデータセットを作り主成分分析を行うと、上図のように群間で差のある結果となります。この場合、ある現象を捉える為に測定したメタボロームデータ全体で差があることが確認された、と結論付けるのは誤りです。このように、扱うデータセットや変数選択などの前処理によって、主成分分析の結果の意味が大きく異なってきます。

メタボロームデータから最大限情報を引き出す為には、問題を良く理解した生物学の研究者と統計科学の研究者が一緒に問題解決していくことが必要です。今後も、出来るだけ厳密性を失うことなく、問題を抱えた生物学者の直感を説明できるような手法の提案を行うことで、お客様の問題解決の手助けが出来ればと考えています。

第3回は9月に行われる統計関連学会連合大会に参加予定なので、その様子をレポートしたいと思います。